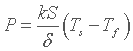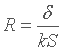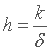The truth about h ...

In order to finally be able to give an interpretation to this coefficient, and for ease of understanding, we will assume that the two boundary layers coincide. We also will assume that the fluid is slowed down so much there that we can consider that the heat exchange is done by pure conduction. Under these circumstances the fluid will behave from the thermal point of view like a solid and the heat transfer will obey the Fourier's Law.
If d is the thickness of the boundary layer (pronounce "delta"), T_s the temperature of the plate and T_f the temperature at the border of the boundary layer (further, the fluid temperature roughly doesn't change) ; then we can write the Fourier's Law for conduction in the boundary layer :

Here S is still the contact surface area between solid and fluid and k is the thermal conductivity of the fluid. Thus thermal resistance can be written :

If we remember the expression of the "true" thermal resistance for convection, seen here, we can finally write :

Lastly, something to chew on in connection with h ! We were looking for high values of h. We can thus interpret (and that's all we can do since this relation is just a trick to understand qualitatively) that the lower d is and the higher k is, the more h is increased.
Concerning k, one would have suspected it, an even more conductive fluid is better ! Concerning d, it means we will seek to have the smallest possible boundary layer thickness. This is the case as the fluid velocity is higher and even more as the flow is turbulent.
Why does turbulence improve convection ? Thanks to the mixing which will homogenize temperature so that temperature variations will be pushed back closer to the solid surface.

Just a little comment, rigorously it would be necessary to talk about thermal conducto-convection, because, as we just saw before, heat exchange between a solid and a fluid simultaneously involve the phenomenon of conduction and convection, both being closely coupled.

But the convective transfer coefficient also depends on viscosity, on density, and on the specific heat of the fluid. Unfortunately to analyze how these properties will influence h it would be necessary to return to a more theoretical analysis, this is not the goal of these articles.
Forget the influence of viscosity, that basically does not change the range of conclusions made here, but it will return when we'll consider pressure drop.
Regarding the specific heat and density, we can dig a little more with the help of another law : the First Principle of Thermodynamics. This principle, whose usefullness is of greater order than the study of h, will enable us to conclude our review of the thermal convection.