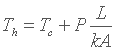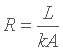A little further...

Let's look more closely at this formula; imagine that the lower surface of the plate is heated with a power P ( as could have been done with a cpu having the same surface area ), the temperature of the hot face is then:

Thus if T_c is given ( to fix ideas one can take ambient air temperature as a reference ); in order to have the lowest temperature T_h, it is necessary to have the lowest thickness, the largest surface area and the highest conductivity.
Concerning thickness and surface area, we will see a little further on that things are not that simple, this simplified Fourier's law is rather limited.
On the other hand for thermal conductivity it is always true; the higher it is, the better it is.
Diamond and silver are the most effective materials but copper has the best conductivity/price ratio, silver is not really of interest considering the slight difference compared to copper and its prohibitive price.

Thermal resistance

Some physical laws express phenomenon which have similar behavior, this is why an analogy with electricity is used : thermal resistance. It states a relation between the temperature difference ( electric voltage ) and the thermal power ( current intensity ), the Fourier's Law is the thermal equivalent of Ohm's Law :

Thermal resistance is measured in °C/W . That's a very significant data because it constitutes the only usable mean of measurement in practice and all heat exchanges will be expressed through this concept. Thermal resistance enables one to measure the effectiveness of a cooling system, this is the data at which it is necessary to look. Keep that in mind while waiting for the part on convection to know some more.

Naturally, we are looking for the smallest possible thermal resistance in order to have the coldest temperature T_h ( nearest to T_c in fact ). For the plate we see that

and we can make the equivalent electric diagram :