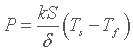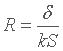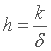La vérité sur h...

Pour finalement pouvoir donner une 'interprétation' à ce coefficient, on va dire en simplifiant, qu'en gros, les deux couches limites coïncident. On va aussi dire que le fluide y est tellement ralenti qu'on peut considérer que les échanges thermiques se font par conduction pure. Alors ce fluide va se comporter du point de vue thermique comme un solide et les transferts de chaleur vont suivre la loi de Fourier pour la conduction !
Si d est son épaisseur ( prononcez "delta" ), T_s la température de la paroi et T_f celle à la frontière de la couche limite ( plus loin de la surface cette température varie peu ) ; alors on peut écrire la loi de Fourier pour la conduction dans la couche limite :

Ici S est toujours la surface de contact entre le solide et le fluide, et k la conductivité thermique du fluide. Donc la résistance thermique peut s'écrire :

Si on se rappelle l'expression de la "vraie" résistance thermique de convection, vue ici, on voit qu'on peut finalement écrire :

Enfin, quelque chose à se mettre sous la dent à propos de h ! Souvenez-vous, on cherchait à avoir h le plus grand possible. On peut donc interpréter ( on ne peut faire que ça puisqu'il ne s'agit pas d'une vraie relation mais juste un truc à la louche pour comprendre qualitativement ) que h est d'autant plus grand que d est faible et que k est grand.
Pour k on s'en serait douté, plus le fluide conduit la chaleur mieux c'est ! Pour d ça veut dire qu'on va rechercher à avoir la couche limite la plus petite possible. C'est le cas quand la vitesse du fluide est de plus en plus grande et d'autant plus lorsque l'écoulement est turbulent.
Pourquoi la turbulence améliore les choses ? grâce au mélange qui va globalement homogénéiser la température de telle sorte que les variations de température seront repoussées plus près des parois.

Petite précision supplémentaire, pour être rigoureux il faudrait parler de conducto-convection thermique, car comme on peut le voir ici les échanges thermiques entre un solide et un fluide font intervenir simultanément les phénomènes de conduction et de convection, les deux étant intimement couplés.

Mais le coefficient de transfert convectif dépend aussi de la viscosité, de la masse volumique et de la chaleur spécifique du fluide. Malheureusement pour analyser comment ces propriétés vont influencer h il faudrait rentrer dans des détails plus théoriques, ce n'est pas le but de ces articles.
Oubliez l'influence de la viscosité, ça ne change pas fondamentalement la portée des conclusions qu'on peut faire ici mais elle reviendra pour les pertes de charges.
En ce qui concerne la chaleur spécifique et la masse volumique, on peut s'en tirer en ayant recourt une autre loi : le premier principe de la thermodynamique. Ce principe, dont l'utilité est d'ordre plus générale que l'étude de h, va nous permettre de conclure sur la convection thermique.